

Next: CIS Energy Equations
Up: Configuration Interaction Singles
Previous: Configuration Interaction Singles
The configuration interaction expansion of an approximate solution to
the electronic Schrödinger equation is typically written
 |
(1) |
 is the so-called ``reference,'' typically obtained from
a Hartree-Fock self-consistent-field (SCF) procedure as the best
single Slater determinant (or configuration state function, CSF) which
describes the electronic state of interest.
is the so-called ``reference,'' typically obtained from
a Hartree-Fock self-consistent-field (SCF) procedure as the best
single Slater determinant (or configuration state function, CSF) which
describes the electronic state of interest.
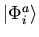 is
the determinant formed by replacing spin-orbital i in
is
the determinant formed by replacing spin-orbital i in
 with spin orbital a, etc. These notes follow the
convention that i,j,k denote orbitals occupied in the reference,
a,b,c denote orbitals unoccupied in the reference, and p,q,r are
general indices. The widely-employed CI singles and doubles
(CISD) wavefunction includes only those N-electron basis
functions which represent single or double substitutions relative to
the reference state and typically accounts for about 95% of the
correlation energy for small molecules near their equilibrium
geometries.
with spin orbital a, etc. These notes follow the
convention that i,j,k denote orbitals occupied in the reference,
a,b,c denote orbitals unoccupied in the reference, and p,q,r are
general indices. The widely-employed CI singles and doubles
(CISD) wavefunction includes only those N-electron basis
functions which represent single or double substitutions relative to
the reference state and typically accounts for about 95% of the
correlation energy for small molecules near their equilibrium
geometries.
Head-Gordon, Pople, and others have advocated the use of configuration
interaction with only single substitutions (CIS) as the starting point
for investigations of excited electronic states. In their 1992 paper,
Foresman, Head-Gordon, Pople, and Frisch [1] list the
following desirable properties of CIS: well defined (and
differentiable), applicable to large systems, size-consistent,
variational, and providing directly comparable (i.e. orthogonal)
electronic state solutions. They go on to present equations for the
CIS energy and gradient when the reference is a single determinant
obtained from an SCF procedure. These notes present a derivation of
the CIS energy for general and several specific types of
single-determinant references. Later, we discuss some extensions
which are necessary for reliable treatments of open-shell systems.


Next: CIS Energy Equations
Up: Configuration Interaction Singles
Previous: Configuration Interaction Singles
C. David Sherrill
2000-04-18
