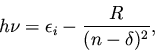 |
(1) |
Rydberg states can be defined as those which fit Eq. (1) and whose wavefunctions are appropriate to generate such a series. Excitation energies are often reported as the difference between the Rydberg state and the corresponding ionization limit; these are referred to as ``term values'' in this context. For theoretical work, it may be more desirable to compute these term values than the actual excitation energies because the Rydberg state should look more like the ion than the ground state; orbital relaxation and correlation effects are more likely to cancel.
While any particular valence transition may also fit Eq. (1),
it will not belong to a series with increasing quantum number n.
An electron in a polyatomic molecule will fit such a formula if it is very
diffuse, so that the core appears as a point charge. Of course this will
never be entirely true, so the parameter ![]() is added to correct for
the extent to which the distant electron penetrates the core. The ground
state of an atom may have an electron with a large radius and may thus
be referred to as a Rydberg state; for neutral polyatomics, this never
happens. Rydberg transitions may be split by core asymmetries, but the
splittings decrease with increasing n because the core becomes better
modeled as a point charge as the electron radius increases.
is added to correct for
the extent to which the distant electron penetrates the core. The ground
state of an atom may have an electron with a large radius and may thus
be referred to as a Rydberg state; for neutral polyatomics, this never
happens. Rydberg transitions may be split by core asymmetries, but the
splittings decrease with increasing n because the core becomes better
modeled as a point charge as the electron radius increases.
For second-row atoms and molecules, the general trends in ![]() are:
are:
The preceeding analysis is of course not directly applicable to polyatmoic
molecules. Indeed, a nonpenetrating AO on one center may still penetrate
another center, suggesting that Rydberg orbitals in polyatomics are
generally more penetrating. The recapitulation idea is now not nearly as
simple, since the Rydberg orbital must be orthogonalized against other
occupied orbitals which may have no overlap with the precursor.
Generally
![]() still holds, but now quantum mechanical exchange has an effect.
still holds, but now quantum mechanical exchange has an effect.
So far, the discussion of penetration has implicitly assumed an effect
of the form
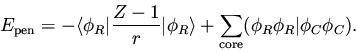 |
(2) |
| (3) |
For polyatomics, the Rydberg states can mix heavily. For NO, 3s is
unperturbed by mixing, but above that ns mixes strongly with
(n-1)d![]() ,
making the nd
,
making the nd![]() series have a negative
series have a negative ![]() .
Actually this makes sense in that
.
Actually this makes sense in that ![]() for nd is about 0 whereas
for nd is about 0 whereas
![]() for ns is about 1.0, so ns and (n-1)d orbitals are about
degenerate. The ns orbitals are a bit lower, so mixing causes the
(n-1)d orbitals to be slightly raised in energy and hence they acquire
a negative
for ns is about 1.0, so ns and (n-1)d orbitals are about
degenerate. The ns orbitals are a bit lower, so mixing causes the
(n-1)d orbitals to be slightly raised in energy and hence they acquire
a negative ![]() (their binding energy becomes slightly smaller
than in hydrogen).
(their binding energy becomes slightly smaller
than in hydrogen).
The singlet-triplet splitting of a pair of Rydberg states should be
small because, at the SCF level, this splitting is roughly 2K, and
for Rydberg states the exchange integral should be relatively small.
In most polyatomic molecules, the singlet-triplet splitting of Rydberg
states is typically less than 5000 cm-1. One exception to this
rule is found found for ethylene, where the
![]() singlet Rydberg configuration is strongly mixed with the singlet valence
configuration
singlet Rydberg configuration is strongly mixed with the singlet valence
configuration
![]() .
However, the correspoding triplet
configurations are not mixed, and thus the singlet-triplet splitting is
not given by something like 2K.
.
However, the correspoding triplet
configurations are not mixed, and thus the singlet-triplet splitting is
not given by something like 2K.
For polyatomics there is an additional difficulty in determining whether
an orbital is Rydberg or unoccupied valence; for example, in methane
the carbon 3s orbital has the same nodal structure as the antibonding
![]() orbital. Such orbitals are called a conjugate pair. Mulliken
claims that these are alternative descriptions of the same orbital;
however, Robin argues that in the above example the 3s orbital is
nonbonding while
orbital. Such orbitals are called a conjugate pair. Mulliken
claims that these are alternative descriptions of the same orbital;
however, Robin argues that in the above example the 3s orbital is
nonbonding while ![]() is antibonding and that numerous calculations
support the idea of separate valence and Rydberg states. In ethylene,
the valence shell
is antibonding and that numerous calculations
support the idea of separate valence and Rydberg states. In ethylene,
the valence shell
![]() .
and Rydberg
.
and Rydberg
![]() configurations have the same nodal patterns, and the V state has been
attributed to each of these separately. Now the prevailing view is
that the state does not fit the Rydberg formula and is primarily a
valence transition with some Rydberg character mixed in. In the triplet
manifold, the analogous configurations give rise to distinct valence and
Rydberg states. If mixing of the conjugate pair is large, then it
can in fact add a node to the Rydberg orbital, which makes it possible
to describe the orbital as n+1 instead of n (and this is the
practice of some authors). However, the size of the orbital and the frequency
from Eq. (1) is much closer to that expected for n.
configurations have the same nodal patterns, and the V state has been
attributed to each of these separately. Now the prevailing view is
that the state does not fit the Rydberg formula and is primarily a
valence transition with some Rydberg character mixed in. In the triplet
manifold, the analogous configurations give rise to distinct valence and
Rydberg states. If mixing of the conjugate pair is large, then it
can in fact add a node to the Rydberg orbital, which makes it possible
to describe the orbital as n+1 instead of n (and this is the
practice of some authors). However, the size of the orbital and the frequency
from Eq. (1) is much closer to that expected for n.
Oscillator strengths of Rydberg transitions are governed by the transition
moment matrix element
| (4) |
The following generalizations are given for Rydberg transitions converging on ionization potentials other than the first:
Experimentally, one way to distinguish between valence and Rydberg excitations
is that the Rydberg excitations can be sensitive to a ``perturber gas.''
This is rationalized by the diffuse nature of the excited electron. Dramatic
effects can be produced by perturber gasses with partial pressures of
only ![]() atm. Of great value is the fact that the perturber gas
causes pressure broadening of the absorber only to higher frequencies.
In contrast, using higher concentrations of the absorber gas (the perturber
is the absorber) causes pressure broadening to higher and lower frequencies
of both Rydberg and valence excitations. In cases where the excitations
appear as continuous bands, the pressure effect is useless unless it is
greatly magnified; this can be accomplished by trapping the absorber in
a low-temperature rare-gas matrix, by dissolving it in a transmitting solvent,
or by forming a polycrystalline film of the neat absorber at low temperatures.
The lowest Rydberg excitation energy of a dilute guest molecule in a rare-gas
host will increase by 2000-5000 cm-1 compared to the gas-phase spectrum,
and the vibronic bandwidths will be 200-500 cm-1. By contrast,
most valence shell excitations will experience a redshift of
1000-3000 cm-1. If placed in a low-mobility organic matrix, valence
excitations behave similarly but Rydberg excitations can broaden sufficiently
as to disappear. The V state of ethylene behaves as a valence excitation
under perturbations. For diatomics and presumably for polyatomics,
in condensed phases coupled Rydberg and valence states can become uncoupled.
atm. Of great value is the fact that the perturber gas
causes pressure broadening of the absorber only to higher frequencies.
In contrast, using higher concentrations of the absorber gas (the perturber
is the absorber) causes pressure broadening to higher and lower frequencies
of both Rydberg and valence excitations. In cases where the excitations
appear as continuous bands, the pressure effect is useless unless it is
greatly magnified; this can be accomplished by trapping the absorber in
a low-temperature rare-gas matrix, by dissolving it in a transmitting solvent,
or by forming a polycrystalline film of the neat absorber at low temperatures.
The lowest Rydberg excitation energy of a dilute guest molecule in a rare-gas
host will increase by 2000-5000 cm-1 compared to the gas-phase spectrum,
and the vibronic bandwidths will be 200-500 cm-1. By contrast,
most valence shell excitations will experience a redshift of
1000-3000 cm-1. If placed in a low-mobility organic matrix, valence
excitations behave similarly but Rydberg excitations can broaden sufficiently
as to disappear. The V state of ethylene behaves as a valence excitation
under perturbations. For diatomics and presumably for polyatomics,
in condensed phases coupled Rydberg and valence states can become uncoupled.