

Next: Matrix Version
Up: Decoupling of Equations in
Previous: Decoupling of Equations in
Now imagine that we have a problem where the wavefunction can be expanded
as a sum of only two basis functions (admittedly unlikely, but perhaps
useful for a single electron spin problem):
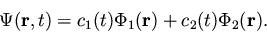 |
(32) |
This leads to the time-dependent Schrödinger equation (where we will
suppress variables 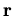 and t for convenience):
and t for convenience):
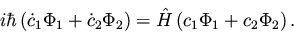 |
(33) |
How do we solve this equation? It's a coupled differential
equation, similar to eq. 1 except that it's first-order
instead of second order. Just as in the classical example, it's the
coupling that makes it hard to solve! In the classical case, the answer
to coupling was to get the eigenfunctions. What happens if we assume
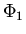 and
and 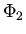 to be eigenfunctions of
to be eigenfunctions of 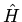 ? In that case,
? In that case,
and the time-dependent equation becomes
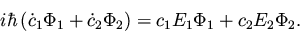 |
(36) |
Furthermore, since the eigenvectors of a Hermitian operator are or can be made
orthogonal, we can multiply by 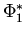 and
and 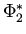 and integrate over
dr to obtain
and integrate over
dr to obtain
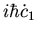 |
= |
c1 E1 |
(37) |
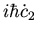 |
= |
c2 E2 |
(38) |
which are simple first-order differential equations solved by
| c1(t) |
= |
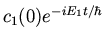 |
(39) |
| c2(t) |
= |
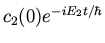 |
(40) |
as you can verify by substituting and differentiating.
But what if our original wavefunction
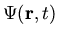 is not given
as a linear combination of eigenfunctions? A good strategy is to re-write
it so that it is! In the coordinate representation (i.e.,
is not given
as a linear combination of eigenfunctions? A good strategy is to re-write
it so that it is! In the coordinate representation (i.e., 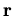 space),
we can get the coefficients ci(0) in an expansion over
orthogonal eigenfunctions
space),
we can get the coefficients ci(0) in an expansion over
orthogonal eigenfunctions
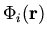 simply as
simply as
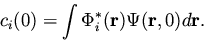 |
(41) |
The other strategy would be to try to re-write the propagator in the
original basis set. In the problems we do, we will usually use the first
approach.


Next: Matrix Version
Up: Decoupling of Equations in
Previous: Decoupling of Equations in
C. David Sherrill
2000-05-02
![]() is not given
as a linear combination of eigenfunctions? A good strategy is to re-write
it so that it is! In the coordinate representation (i.e.,
is not given
as a linear combination of eigenfunctions? A good strategy is to re-write
it so that it is! In the coordinate representation (i.e., ![]() space),
we can get the coefficients ci(0) in an expansion over
orthogonal eigenfunctions
space),
we can get the coefficients ci(0) in an expansion over
orthogonal eigenfunctions
![]() simply as
simply as