

Next: Dirac Notation Version
Up: Decoupling of Equations in
Previous: Basis Functions in Coordinate
We can use matrix notation to re-do the problem above. The time-dependent
Schrödinger equation in the original
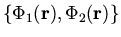 basis becomes
basis becomes
![$\displaystyle i \hbar \left[ \begin{array}{c} {\dot c}_1 \\ {\dot c}_2 \end{ar...
...2} \end{array} \right]
\left[ \begin{array}{c} c_1 \\ c_2 \end{array} \right].$](img94.png) |
|
|
(42) |
Now, just as in eq. 3, we can see that if H was
a diagonal matrix, then the equations for c1 and c2 would become
decoupled. Again, we can make H diagonal by going to the special
basis made of the eigenvectors of H. In this new basis, we will denote
vector coefficients and matrix elements with tildes as a reminder that
the basis set has changed, and we obtain:
![$\displaystyle i \hbar \left[ \begin{array}{c}
{\dot {\tilde c}}_1 \\ {\dot {\t...
...ght]
\left[ \begin{array}{c}
{\tilde c}_1 \\ {\tilde c}_2 \end{array} \right].$](img95.png) |
|
|
(43) |
Now remember that we've gone to the eigenvector basis (which we'll also
denote with tildes to distinguish it from the original basis), so we know that
Thus we can further simplify the diagonal elements as
for normalized basis functions. Likewise of course
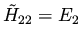 .
Hence, we can expand our matrix equation 43 as
.
Hence, we can expand our matrix equation 43 as
which is the same thing we got before when we assumed the given
functions were orthonormal. The only difference is that here we emphasized
the diagonalization of H rather than getting the eigenvectors, but of
course it is the same process. These decoupled equations can be
solved the same way as before to give
which we could write back in matrix notation (still in the eigenvector
or tilde basis) as
![$\displaystyle \left[ \begin{array}{c}
{\tilde c}_1(t) \\ {\tilde c}_2(t) \end{array} \right]$](img112.png) |
= |
![$\displaystyle \left[ \begin{array}{cc}
e^{- i E_1 t / \hbar} & 0 \\
0 & e^{- i...
...left[ \begin{array}{c} {\tilde c}_1(0) \\ {\tilde c}_2(0) \end{array}\right] .$](img113.png) |
(51) |
We can identify the matrix as the propagator,
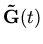 |
= |
![$\displaystyle \left[ \begin{array}{cc}
e^{- i E_1 t / \hbar} & 0 \\
0 & e^{- i E_2 t / \hbar} \end{array} \right]$](img115.png) |
(52) |
in the eigenvector basis.
In the vector/matrix representation, we can go from our original to our
tilde coefficients and back as
where 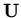 is the matrix made by making each column an eigenvector
of
is the matrix made by making each column an eigenvector
of 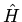 in the original basis. We could transform our propagator
in the original basis. We could transform our propagator
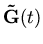 from the eigenvector basis to the original basis by
from the eigenvector basis to the original basis by
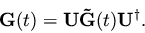 |
(55) |


Next: Dirac Notation Version
Up: Decoupling of Equations in
Previous: Basis Functions in Coordinate
C. David Sherrill
2000-05-02
![$\displaystyle i \hbar \left[ \begin{array}{c} {\dot c}_1 \\ {\dot c}_2 \end{ar...
...2} \end{array} \right]
\left[ \begin{array}{c} c_1 \\ c_2 \end{array} \right].$](img94.png)
![$\displaystyle i \hbar \left[ \begin{array}{c} {\dot c}_1 \\ {\dot c}_2 \end{ar...
...2} \end{array} \right]
\left[ \begin{array}{c} c_1 \\ c_2 \end{array} \right].$](img94.png)
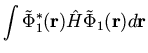
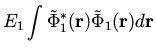
![$\displaystyle \left[ \begin{array}{c}
{\tilde c}_1(t) \\ {\tilde c}_2(t) \end{array} \right]$](img112.png)
![$\displaystyle \left[ \begin{array}{cc}
e^{- i E_1 t / \hbar} & 0 \\
0 & e^{- i...
...left[ \begin{array}{c} {\tilde c}_1(0) \\ {\tilde c}_2(0) \end{array}\right] .$](img113.png)
![$\displaystyle \left[ \begin{array}{c} c_1(t) \\ c_2(t) \end{array} \right]$](img116.png)
![$\displaystyle {\bf U} \left[ \begin{array}{c}
{\tilde c}_1(t) \\ {\tilde c}_2(t) \end{array} \right]$](img117.png)
![$\displaystyle \left[ \begin{array}{c}
{\tilde c}_1(t) \\ {\tilde c}_2(t) \end{array} \right]$](img112.png)
![$\displaystyle {\bf U}^{\dagger}
\left[ \begin{array}{c} c_1(t) \\ c_2(t) \end{array} \right],$](img118.png)