

Next: Unrestricted Hartree-Fock References
Up: CIS Energy Equations
Previous: CIS Energy Equations
Now consider the case of a closed-shell RHF reference determinant.
In this case,
 ,
so that
,
so that  becomes zero.
becomes zero.
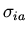 simplifies to
simplifies to
 |
(23) |
Conserving Ms requires that the spins of j and b are equal. Therefore,
 |
(24) |
After integrating over spin, this becomes in chemists' notation
 |
(25) |
Time-reversal symmetry imposes certain conditions on the CI
coefficients. In alpha and beta string notation [5], for
Ms=0 cases,
 |
(26) |
An analogous equation also holds for 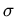 .
This means that for a
closed shell RHF reference,
.
This means that for a
closed shell RHF reference,
 (
(
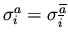 )
for singlets,
and
)
for singlets,
and
 (
(
 )
for triplets; thus only half
of the CI coefficients must be computed explicitly. These sign rules
are also evident from the observation that
)
for triplets; thus only half
of the CI coefficients must be computed explicitly. These sign rules
are also evident from the observation that
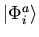 and
and
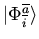 are not spin
eigenfunctions, but that the total CI wavefunction will be a spin
eigenfunction (if the required determinants are present in the CI
space). Using the determinant sign convention of Szabo and Ostlund
[6], spin eigenfunctions (or CSFs) associated with
the above determinants are
are not spin
eigenfunctions, but that the total CI wavefunction will be a spin
eigenfunction (if the required determinants are present in the CI
space). Using the determinant sign convention of Szabo and Ostlund
[6], spin eigenfunctions (or CSFs) associated with
the above determinants are
Using these relationships between CI coefficients, we obtain
Furthermore,
 and
and
 .
.
Consider how equations
(20)-(22) change when spin is
explicitly accounted for. There will be two pseudodensity matrices,
Due to equation (26),
 for singlets,
and
for singlets,
and
 for triplets. Thus it is necessary to form only one
of the Fock-like matrices,
for triplets. Thus it is necessary to form only one
of the Fock-like matrices,
 or
or
 .
The former is constructed as
.
The former is constructed as
Finally
 is constructed according to eq
(22). In terms of these quantities, the
is constructed according to eq
(22). In terms of these quantities, the
 vector can be written
vector can be written


Next: Unrestricted Hartree-Fock References
Up: CIS Energy Equations
Previous: CIS Energy Equations
C. David Sherrill
2000-04-18




![$\displaystyle c_i^a (\epsilon_a - \epsilon_i)
+ \sum_{jb} c_j^b \left[ 2 (ai \vert jb) - (ab \vert ji) \right]$](img65.png)

![$\displaystyle \sum_{\lambda \sigma}
\left[
2 (\mu \nu \vert \lambda \sigma)
- (\mu \sigma \vert \lambda \nu)
\right] {\tilde P}_{\lambda \sigma}^{\alpha}$](img79.png)
