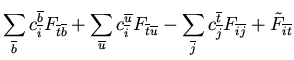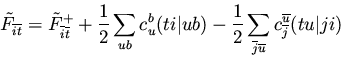

Next: Extensions of CIS to
Up: CIS Energy Equations
Previous: Unrestricted Hartree-Fock References
A single-determinant restricted open-shell Hartree-Fock (ROHF) wavefunction
describing a high-spin open-shell system will be an eigenfunction
of
 (i.e., a CSF). This is easy to verify by direct
application of the
(i.e., a CSF). This is easy to verify by direct
application of the
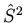 operator, which is
operator, which is
where
and
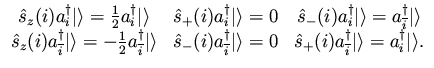 |
|
|
(50) |
The high-spin ROHF wavefunction can be written as
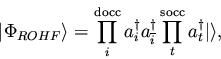 |
(51) |
where t and u will denote open-shells. Applying
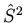 ,
this becomes
,
this becomes
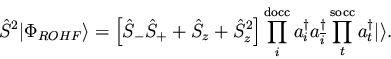 |
(52) |
This is easy to evaluate:
The raising operator
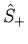 yields zero when acting on
yields zero when acting on
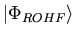 :
raising operators applied to
:
raising operators applied to  electrons
always yield zero, and raising operators applied to the
electrons
always yield zero, and raising operators applied to the 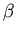 electrons yield
electrons yield 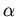 spin orbitals which are already occupied (so
the determinant vanishes by the Pauli principle). Hence the final
result is
spin orbitals which are already occupied (so
the determinant vanishes by the Pauli principle). Hence the final
result is
where
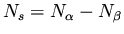 .
.
Now it is worthwhile to consider how to form CSFs for the single
excitations. Determinants which promote electrons from the
singly-occupied space to the virtual space, as well as determinants
which promote 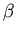 electrons in the doubly-occupied orbitals to the
singly-occupied orbitals, are already spin-adapted (the proof is
completely analogous to that above for the ROHF reference
determinant). The only other relevant single excitations are those
which move an electron from a doubly-occupied orbital to a virtual
orbital. These determinants are not spin-adapted, as we will
proceed to demonstrate. Consider the action of
electrons in the doubly-occupied orbitals to the
singly-occupied orbitals, are already spin-adapted (the proof is
completely analogous to that above for the ROHF reference
determinant). The only other relevant single excitations are those
which move an electron from a doubly-occupied orbital to a virtual
orbital. These determinants are not spin-adapted, as we will
proceed to demonstrate. Consider the action of
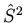 on the
determinant
on the
determinant
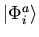 :
:
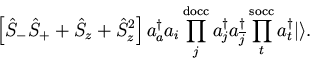 |
(56) |
The result of
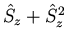 is easily determined to be
is easily determined to be
![\begin{displaymath}\left[ {\hat S}_z + {\hat S}_z^2 \right] \vert \Phi_i^a \rang...
...ft( \frac{N_s}{2} + 1 \right) \right]
\vert \Phi_i^a \rangle.
\end{displaymath}](img136.png) |
(57) |
Now all that remains is the raising and lowering operators. These are
somewhat more involved and require that attention be paid to the
sign.
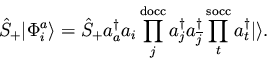 |
(58) |
By arguments similar to those presented above, all raising operators
yield zero except for
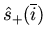 .
Using the
anticommutation relations for creation and annihilation operators,
.
Using the
anticommutation relations for creation and annihilation operators,
The
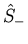 operator can now affect electrons in any of the
following orbitals: a, i, and any of the open-shell orbitals.
operator can now affect electrons in any of the
following orbitals: a, i, and any of the open-shell orbitals.
Thus overall,
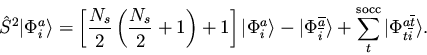 |
(61) |
The analogous equation for
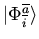 is
is
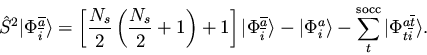 |
(62) |
Clearly a spin eigenfunction can be constructed as
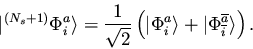 |
(63) |
Then the operation of
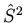 is
is
![\begin{displaymath}{\hat S}^2 \vert ^{(N_s+1)}\Phi_i^a \rangle
= \left[ \frac{N...
...N_s}{2} + 1 \right) \right]
\vert ^{(N_s+1)}\Phi_i^a \rangle.
\end{displaymath}](img151.png) |
(64) |
Now that the relevant CSFs have been obtained, they can be used to
define the ROHF convergence criteria: the final ROHF wavefunction will
not mix with any of the singly substituted CSFs. Thus
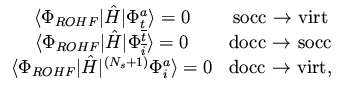 |
|
|
(65) |
which implies the following conditions on the Fock matrix elements
| Fta |
= |
0 |
(66) |
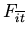 |
= |
0 |
(67) |
| Fia |
= |
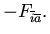 |
(68) |
Using these results, we can write down expressions for the 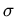 vectors. Since determinants
vectors. Since determinants
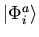 must enter with the same
coefficients as
must enter with the same
coefficients as
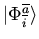 ,
,
 once again. Furthermore, since the ROHF reference cannot mix
with any other singly excited configurations, the c0 contribution
to
once again. Furthermore, since the ROHF reference cannot mix
with any other singly excited configurations, the c0 contribution
to
 and
and
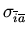 may be
safely ignored. We will therefore consider four cases:
may be
safely ignored. We will therefore consider four cases:
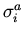 ,
,
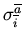 ,
,
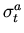 ,
and
,
and
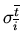 ,
where once again t,u represent
singly occupied orbitals.
,
where once again t,u represent
singly occupied orbitals.
The equation for
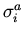 is readily seen to be
is readily seen to be
Separating the Fock operator terms from the two-electron integrals,
and integrating out spin, this yields
where we have used the relation
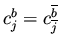 .
The analogous equation for
.
The analogous equation for 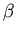 spins is
spins is
If the equality
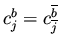 is to be
maintained, we must have
is to be
maintained, we must have
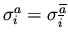 .
It is then computationally
convenient to form these quantities as
.
It is then computationally
convenient to form these quantities as
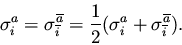 |
(72) |
Thus
Now it is clear that the two-electron integrals can be treated all
together. To begin condensing the notation once again, let us define
the following quantities:
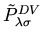 |
= |
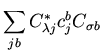 |
(74) |
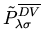 |
= |
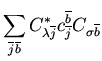 |
(75) |
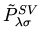 |
= |
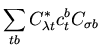 |
(76) |
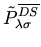 |
= |
 |
(77) |
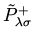 |
= |
![$\displaystyle \frac{1}{2} \left[
{\tilde P}_{\lambda \sigma}^{DV}
+ {\tilde P}_...
... P}_{\lambda \sigma}^{SV}
+ {\tilde P}_{\lambda \sigma}^{\overline{DS}}
\right]$](img179.png) |
(78) |
where
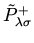 the same as that defined in eq. (17)
of Maurice and Head-Gordon [2].
Then
the same as that defined in eq. (17)
of Maurice and Head-Gordon [2].
Then
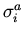 can be evaluated as
can be evaluated as
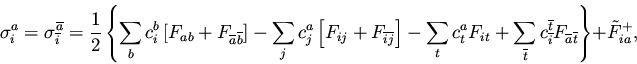 |
(79) |
where
Next consider the term
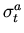 :
:
It is computationally more efficient to evaluate
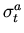 at the
same time as
at the
same time as
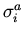 .
The value of
.
The value of
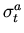 computed in this
manner must of course be corrected for the difference in the formulas
for
computed in this
manner must of course be corrected for the difference in the formulas
for
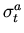 and
and
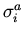 ,
but this correction scales as only
,
but this correction scales as only
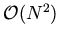 (see Maurice and Head-Gordon [2]). The
two-electron part is thus computed by
(see Maurice and Head-Gordon [2]). The
two-electron part is thus computed by
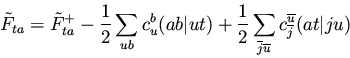 |
(83) |
Similar considerations apply to
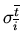 ,
which is
,
which is
where
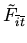 is actually evaluated
according to
is actually evaluated
according to
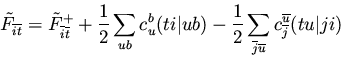 |
(85) |


Next: Extensions of CIS to
Up: CIS Energy Equations
Previous: Unrestricted Hartree-Fock References
C. David Sherrill
2000-04-18
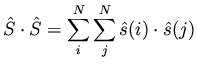
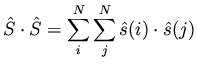
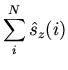
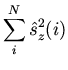
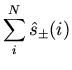
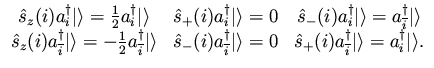
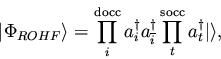
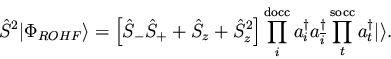

![$\displaystyle \left[ \frac{1}{2}(N_{\alpha} - N_{\beta}) \right]
\prod_{i}^{\rm...
...} a_{\overline{i}}^{\dagger}
\prod_{t}^{\rm socc} a_{t}^{\dagger} \vert \rangle$](img125.png)
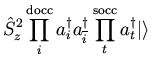
![$\displaystyle \left[ \frac{1}{2}(N_{\alpha} - N_{\beta}) \right]^2
\prod_{i}^{\...
... a_{\overline{i}}^{\dagger}
\prod_{t}^{\rm socc} a_{t}^{\dagger} \vert \rangle.$](img127.png)
![$\displaystyle \left[ \frac{1}{4} (N_{\alpha} - N_{\beta})^2
+ \frac{1}{2} (N_{\alpha} - N_{\beta})
\right] \vert \Phi_{ROHF} \rangle$](img131.png)
![$\displaystyle \left[ \frac{1}{2} N_s \left( \frac{1}{2} N_s + 1 \right) \right]
\vert \Phi_{ROHF} \rangle,$](img132.png)
![]() electrons in the doubly-occupied orbitals to the
singly-occupied orbitals, are already spin-adapted (the proof is
completely analogous to that above for the ROHF reference
determinant). The only other relevant single excitations are those
which move an electron from a doubly-occupied orbital to a virtual
orbital. These determinants are not spin-adapted, as we will
proceed to demonstrate. Consider the action of
electrons in the doubly-occupied orbitals to the
singly-occupied orbitals, are already spin-adapted (the proof is
completely analogous to that above for the ROHF reference
determinant). The only other relevant single excitations are those
which move an electron from a doubly-occupied orbital to a virtual
orbital. These determinants are not spin-adapted, as we will
proceed to demonstrate. Consider the action of
![]() on the
determinant
on the
determinant
![]() :
:
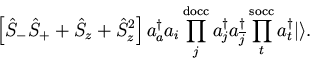
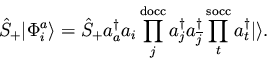
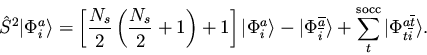
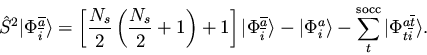
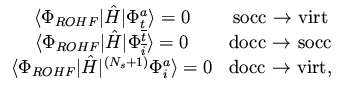
![]() vectors. Since determinants
vectors. Since determinants
![]() must enter with the same
coefficients as
must enter with the same
coefficients as
![]() ,
,
![]() once again. Furthermore, since the ROHF reference cannot mix
with any other singly excited configurations, the c0 contribution
to
once again. Furthermore, since the ROHF reference cannot mix
with any other singly excited configurations, the c0 contribution
to
![]() and
and
![]() may be
safely ignored. We will therefore consider four cases:
may be
safely ignored. We will therefore consider four cases:
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() ,
where once again t,u represent
singly occupied orbitals.
,
where once again t,u represent
singly occupied orbitals.
![]() is readily seen to be
is readily seen to be
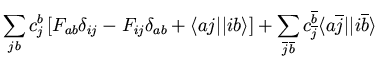

![$\displaystyle \sum_{jb} c_j^b \left[ F_{ab} \delta_{ij} - F_{ij} \delta_{ab} \r...
...t} \delta_{ab}
+ \sum_{jb} c_j^b \left[ 2 (ai \vert jb) - (ab \vert ji) \right]$](img160.png)
![$\displaystyle \sum_{tb} c_t^b \left[ 2 (ai \vert tb) - (ab \vert ti) \right]
+ \sum_{\overline{j}\overline{t}} c_{\overline{j}}^{\overline{t}}
(ai \vert jt),$](img161.png)
![$\displaystyle \sum_{\overline{j}\overline{b}} c_{\overline{j}}^{\overline{b}}
\...
... c_{\overline{j}}^{\overline{b}}
\left[ 2 (ai \vert jb) - (ab \vert ji) \right]$](img164.png)
![$\displaystyle \sum_{tb} c_t^b (ai \vert tb)
+ \sum_{\overline{j}\overline{t}} c_{\overline{j}}^{\overline{t}}
\left[ 2 (ai \vert jt) - (at \vert ji) \right],$](img165.png)
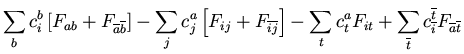
![$\displaystyle \sum_{jb} c_j^b \left[ 2 (ai \vert jb) - (ab \vert ji) \right]
+ ...
... c_{\overline{j}}^{\overline{b}}
\left[ 2 (ai \vert jb) - (ab \vert ji) \right]$](img169.png)
![$\displaystyle \sum_{tb} c_t^b \left[ 2 (ai \vert tb) - (ab \vert ti) \right]
+ ...
...c_{\overline{j}}^{\overline{t}}
\left[ 2 (ai \vert jt) - (at \vert ji) \right].$](img170.png)
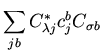
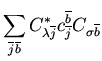
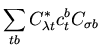

![$\displaystyle \frac{1}{2} \left[
{\tilde P}_{\lambda \sigma}^{DV}
+ {\tilde P}_...
... P}_{\lambda \sigma}^{SV}
+ {\tilde P}_{\lambda \sigma}^{\overline{DS}}
\right]$](img179.png)
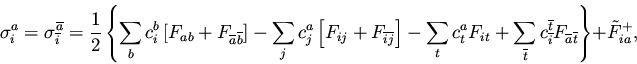
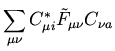
![$\displaystyle \sum_{\lambda \sigma}
\left[
2 (\mu \nu \vert \lambda \sigma)
- (\mu \sigma \vert \lambda \nu)
\right]
{\tilde P}_{\lambda \sigma}^{+}$](img185.png)
![]() :
:
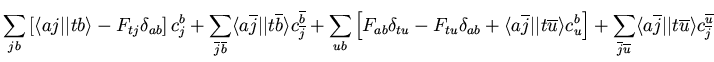
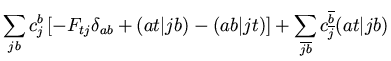
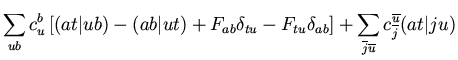
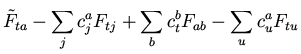
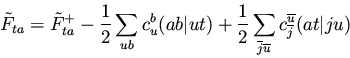
![]() ,
which is
,
which is
![$\displaystyle \sum_{jb} c_j^b \langle \overline{t} j \vert\vert \overline{i} b ...
... \overline{t} \overline{j} \vert\vert \overline{i} \overline{u} \rangle
\right]$](img194.png)
![$\displaystyle \sum_{\overline{b}} c_{\overline{i}}^{\overline{b}}
F_{\overline{...
...}} c_{\overline{j}}^{\overline{b}}
\left[ (ti \vert jb) - (tb \vert ji) \right]$](img195.png)
![$\displaystyle \sum_{ub} c_u^b (ti \vert ub)
+ \sum_{\overline{j} \overline{u}} c_{\overline{j}}^{\overline{u}}
\left[ (ti \vert ju) - (tu \vert ji) \right]$](img196.png)