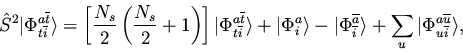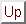

Next: Bibliography
Up: Configuration Interaction Singles
Previous: Restricted Open-Shell Hartree-Fock References
The ROCIS method appears to be superior to UCIS for open-shell
molecules [2]. Nevertheless, ROCIS is not as reliable
for open-shell cases as RCIS is for closed-shell cases. As explained
by Maurice and Head-Gordon [7], a careful analysis of
the failures of ROCIS indicated that certain double substitutions
which are neglected in UCIS and ROCIS can of crucial importance in
open-shell systems. The spin-adapted configurations are of the form:
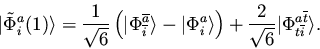 |
(86) |
Although the third determinant is a double substitution as far as
spin-orbitals are concerned, it is only a single substitution when
spatial orbital occupations are considered. Hence, it is very
reasonable to assume that this CSF may be of comparable importance to
the singles included in ROCIS. The extended CIS method (XCIS) is a
spin-adapted CI method including these ``extended single''
substitutions.
It is helpful to first verify that eq. (86) is indeed
an eigenfunction of
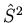 .
Using previous results for ROCIS,
it is trivial to see that
.
Using previous results for ROCIS,
it is trivial to see that
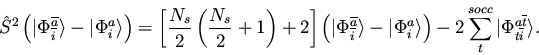 |
(87) |
It remains to be seen what is the effect of
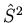 acting on
acting on
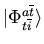 .
.
The factor
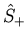 acts on unpaired
acts on unpaired 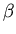 spins; thus,
spins; thus,
The result of
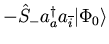 has already been worked out in eq. (60).
Thus overall,
has already been worked out in eq. (60).
Thus overall,
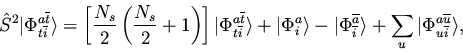 |
(90) |
and it is easy to see that
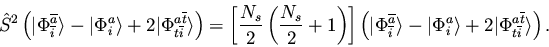 |
(91) |
Hence
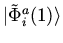 (eq. 86) is a CSF.
(eq. 86) is a CSF.


Next: Bibliography
Up: Configuration Interaction Singles
Previous: Restricted Open-Shell Hartree-Fock References
C. David Sherrill
2000-04-18
![]() .
Using previous results for ROCIS,
it is trivial to see that
.
Using previous results for ROCIS,
it is trivial to see that
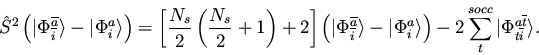
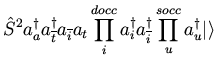
![$\displaystyle {\hat S}_{-} {\hat S}_{+} \vert \Phi_{t \overline{i}}^{a \overlin...
...s}{2} + 1 \right) \right]
\vert \Phi_{t \overline{i}}^{a \overline{t}} \rangle.$](img205.png)