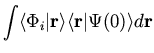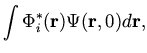

Next: About this document ...
Up: Decoupling of Equations in
Previous: Matrix Version
Let us do the same problem yet again in Dirac or Bracket notation. For this
version, let's go ahead and assume that we expand our state function
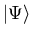 directly in terms of the Hamiltonian eigenvectors
directly in terms of the Hamiltonian eigenvectors
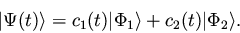 |
(56) |
When substituted into the time-dependent Schrödinger equation, this
gives
Now multiply on the left by
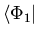 and
and
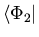 ,
respectively,
and use
,
respectively,
and use
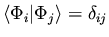 to obtain
to obtain
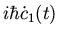 |
= |
E1 c1(t) |
(58) |
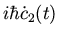 |
= |
E2 c2(t), |
(59) |
just as before, with solutions once again
| c1(t) |
= |
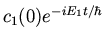 |
(60) |
| c2(t) |
= |
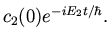 |
(61) |
But what if we are given
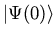 in a form that looks different
from that of eq. 56? Since the eigenvector basis must
be complete (although it will usually have more than two basis vectors,
as in this example!), we can always rewrite our state vector in this form,
and the coefficients can always be computed as
in a form that looks different
from that of eq. 56? Since the eigenvector basis must
be complete (although it will usually have more than two basis vectors,
as in this example!), we can always rewrite our state vector in this form,
and the coefficients can always be computed as
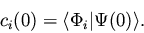 |
(62) |
Note that in this subsection we aren't assuming anything about whether we
are working in coordinate (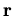 )
space or momentum (
)
space or momentum (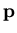 )
space
or some other space. However, if we were working in coordinate space,
we could insert the resolution of the identity
)
space
or some other space. However, if we were working in coordinate space,
we could insert the resolution of the identity
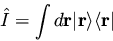 |
(63) |
to obtain
| ci(0) |
= |
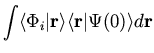 |
|
| |
= |
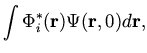 |
(64) |
completely consistent with everything above.
The propagator may be written as
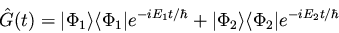 |
(65) |
again with
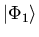 and
and
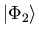 here representing
eigenfunctions of
here representing
eigenfunctions of 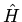 with eigenvalues E1 and E2, respectively.
Note the similarity between this propagator and that from the classical
example in eq. 27. The only real difference
is that there, we chose to work with cosines as a phase factor, and here
we are using the more general exponential. Evidently the frequency here
is represented by
with eigenvalues E1 and E2, respectively.
Note the similarity between this propagator and that from the classical
example in eq. 27. The only real difference
is that there, we chose to work with cosines as a phase factor, and here
we are using the more general exponential. Evidently the frequency here
is represented by
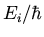 .
You can verify that in the eigenvector basis, this operator becomes
.
You can verify that in the eigenvector basis, this operator becomes
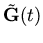 from eq. 52 in the previous section.
Hopefully you can also see that in the eigenvector basis this definition
is equivalent to the more general form 31.
from eq. 52 in the previous section.
Hopefully you can also see that in the eigenvector basis this definition
is equivalent to the more general form 31.


Next: About this document ...
Up: Decoupling of Equations in
Previous: Matrix Version
C. David Sherrill
2000-05-02
![]() in a form that looks different
from that of eq. 56? Since the eigenvector basis must
be complete (although it will usually have more than two basis vectors,
as in this example!), we can always rewrite our state vector in this form,
and the coefficients can always be computed as
in a form that looks different
from that of eq. 56? Since the eigenvector basis must
be complete (although it will usually have more than two basis vectors,
as in this example!), we can always rewrite our state vector in this form,
and the coefficients can always be computed as